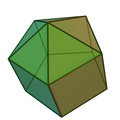
五角錐柱
外觀
 | |||
| 類別 | 棱錐柱 詹森多面體 J8 - J9 - J10 | ||
|---|---|---|---|
| 對偶多面體 | 五角錐柱(自身對偶) | ||
| 識別 | |||
| 鮑爾斯縮寫 | epeppy | ||
| 數學表示法 | |||
| 康威表示法 | P5+Y5 | ||
| 性質 | |||
| 面 | 11 | ||
| 邊 | 20 | ||
| 頂點 | 11 | ||
| 歐拉特徵數 | F=11, E=20, V=11 (χ=2) | ||
| 組成與佈局 | |||
| 面的種類 | 三角形×5 正方形×5 五邊形×1 | ||
| 頂點佈局 | 5(42.5) 5(32.42) | ||
| 對稱性 | |||
| 對稱群 | C5v, [5], (*55) C5v群 | ||
| 旋轉對稱群 | C5, [5]+, (55) | ||
| 特性 | |||
| 凸、demi-regular | |||
| 圖像 | |||
| |||
在幾何學中,五角錐柱是指底面為五邊形的錐柱體,或是將底面全等的五角錐與五角柱疊合所形成的立體。若底面為正五邊形則稱為正五角錐柱。五角錐柱具有11個面、20個邊、和11個頂點,每個五角錐柱皆為一個十一面體。
詹森多面體
[編輯]考慮一個正五角錐柱,若每一個面皆為正多邊形,則為92種詹森多面體(J9)中的其中一個,也是錐柱體的一種,可由詹森多面體中的正五角錐與柏拉圖立體中的半正五面體於相等大小的五邊形面接合而組成。這92種詹森多面體最早在1966年由詹森·諾曼(Norman Johnson)命名並給予描述。
相關多面體
[編輯]| 二角錐柱 | 三角錐柱 | 四角錐柱 | 五角錐柱 | 六角錐柱 | 七角錐柱 | ... | 圓錐柱 |
|---|---|---|---|---|---|---|---|

|

|

|

|

|

|
|
參見
[編輯]| 這是一篇與多面體相關的小作品。您可以透過編輯或修訂擴充其內容。 |