正六百胞体

正六百胞体 （600胞体）
类型	正多胞体
家族	类二十面体形
对偶多胞形	正一百二十胞体
识别
鲍尔斯缩写	ex
数学表示法
考克斯特符号
施莱夫利符号	{3,3,5}
性质
胞	600 (3.3.3)
面	1200 {3}
边	720
顶点	120
组成与布局
顶点图	(3.3.3.3.3)
对称性
对称群	H4, [3,3,5]
特性
凸多胞形, 点可递, 边可递, 面可递

二维线架正投射

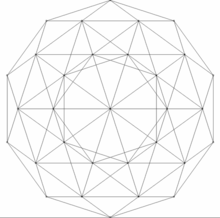
几何学中，正六百胞体（hexacosichoron）是四维凸正多胞体，施莱夫利符号是{3,3,5}，有时候会视为正二十面体的四维类比。

正六百胞体的边界有600个正四面体胞、1200个正三角形面、720条边和120个顶点。每一顶点有20个正四面体相接。

几何性质

正六百胞体的对偶多胞体是正一百二十胞体。 正六百胞体的顶点图是正二十面体。
边长为a的正六百胞体超体积为${\frac {50+25{\sqrt {5}}}{4}}a^{4}$，表体积为50√2a³。

以原点为中心，边长为 1/φ 的正六百胞体（其中φ = (1+√5)/2是黄金比例），顶点坐标如下：16个顶点形式如下

(±½,±½,±½,±½)，

8个顶点从下列坐标不同排列得出

(0,0,0,±1)，

剩下96个顶点是下列坐标的偶置换

½(±1,±φ,±1/φ,0)。

如果一个正六百胞体的棱长为1，则其外接超球半径为${\begin{smallmatrix}{\frac {{\sqrt {5}}+1}{2}}\approx 1.618\end{smallmatrix}}$即黄金分割比；其外中交超球(经过正六百胞体每条棱的中点)半径为${\begin{smallmatrix}{\frac {\sqrt {2{\sqrt {5}}+5}}{2}}\approx 1.538\end{smallmatrix}}$；其内中交超球（经过正六百胞体每个面的中心）半径为${\begin{smallmatrix}{\frac {{\sqrt {15}}+3{\sqrt {3}}}{6}}\approx 1.512\end{smallmatrix}}$；其内切超球半径为${\begin{smallmatrix}{\frac {{\sqrt {10}}+2{\sqrt {2}}}{4}}\approx 1.498\end{smallmatrix}}$ 。

注意到首16个顶点构成超正方体，次8个构成正十六胞体。这24个顶点一起构成正二十四胞体，事实上，如果移除这24个顶点，就会得到另一个有意思的半正多胞体扭棱正二十四胞体（Snub Icositetrachoron）。

对称群构造

如果把坐标看作四元数，正六百胞体的120个顶点以四元数乘法组成群。这个群通常称为双二十面体群，因为它是二十面体群I的双重复盖。这个双十二面体群也可被看作是正六百胞体的旋转（无反射）对称群，因为单位四元数的乘法等同于点的旋转，也因此双十二面体群是H₄群的一个子群。双二十面体群同构于特殊线性群SL(2,5)。

正六百胞体的对称群是H₄的外尔群，这个群的阶是14400。

可视化

正六百胞体的胞众多，并且这些正四面体胞基本上没有什么规律可循，为正六百胞体的可视化带来了许多困难，但作为正一百二十胞体的对偶，许多正一百二十胞体的性质也表现在正六百胞体上。

大圆结构

正一百二十胞体的10个会首尾相连，构成“大圆”，这些胞与正六百胞体的顶点对偶，它们也会互相连接形成一个正十边形，这正十边形的每一条边周围都有5个正四面体共这条边，这种结构看上去就像有棱有角的飞盘。正十边形相邻的两条棱周围的两簇正四面体中间会有空隙，我们可以在填入10个正四面体使其构成正二十面体，这样你就会得到一个涉及150个胞、10条棱、100个裸露的正三角形面的环形结构，我们还可以在向这些面上填上正四面体，会得到一个涉及250个胞的有50个突出的顶点和100条凹陷的棱的大圆，它与另一条与之正交的250胞环在顶点处咬合，剩余的棱的空隙是剩余的100个胞。现在，如果我们去掉这两条大圆最初的10个顶点，我们就会得到四维唯一的非Wythoff凸半正多胞体——重反棱柱，原来的大圆处留下了各10个正五反棱柱，并剩下了300个正四面体胞。

参考

• 600-cell （页面存档备份，存于互联网档案馆） 逐层剖析了正六百胞体的表分层结构
• Regular Convex Four-Dimensional Polytopes提供了正六百胞体的几何数据

四维正多胞体
正五胞体	超立方体	正十六胞体	正二十四胞体	正一百二十胞体	正六百胞体
{3,3,3}	{4,3,3}	{3,3,4}	{3,4,3}	{5,3,3}	{3,3,5}