功 (英語:work ),也叫機械功 ,是物理學 中表示當外界沿物體位移 的方向施加力 時,外界的能量 被轉移到移動的物體身上,因為根據能量守恆定律 ,兩個物體的能量總和不會增加。[ 1] [ 2] 機械能 相似的是,功也是純量 ,意味着有多少能量被轉移[ 1] 國際單位制 單位為焦耳 。
球員對球作正功,使其動能增加。 「功」一詞最初是法國數學家賈斯帕-古斯塔夫·科里奧利 創造的[ 3]
由動能定理 ,若一個外力作用於一物體使之動能 從Ek0 增至Ek ,那麼,此力所作的機械功為:
W
=
Δ
E
k
=
E
k
−
E
k
0
=
1
2
m
(
v
2
−
v
0
2
)
{\displaystyle W=\Delta E_{\rm {k}}=E_{\rm {k}}-E_{\mathrm {k} 0}={\tfrac {1}{2}}m(v^{2}-v_{0}^{2})\,\!}
[ 4] 其中m 是物體的質量,v 是物體的速度。
機械功就是力與位移的內積 :
W
=
F
→
⋅
d
→
{\displaystyle W={\vec {F}}\cdot {\vec {d}}}
[ 5] 若力與位移的夾角小於直角,則機械功為正,亦稱為力作正功。若力與位移的夾角大於直角,則機械功為負,或力作負功,或物體克服力作功。
若力的方向與位移方向垂直,則此力不作功:[ 5]
W
=
0
{\displaystyle W=0}
即使存在力,也可能沒有作功。例如,在等速率圓周運動 中,向心力 沒有作功,因為做圓周運動的物體的動能沒有發生變化。同樣的,桌上的一本書,儘管桌對書有支持力,但因沒有位移而沒有作功。
國際單位制 中功的單位為焦耳 (J)。焦耳被定義為用1牛頓的力對一物體使其發生1米的位移所作的機械功的大小。因次 相同的單位牛·米有時也使用,但是一般牛·米用於力矩 ,使其跟功和能區別開。
非國際單位制單位包括爾格 、英尺·磅、千瓦時(kW·h)、大氣壓力、馬力時(HP·h)。而由於具有相同的物理量─熱能,偶爾會見到以熱量熱能形式表示的測量單位,如:卡路里(cal)、BTU等。
功與能息息相關,根據系統能量的守恆,內部總能量的變化等於添加的熱能加上環境對系統所作的功。見熱力學第一定律 。
d
E
=
δ
Q
+
δ
W
{\displaystyle \mathrm {d} E=\delta Q+\delta W}
1.保守力 作功使「存」在物體中的位能 釋放出來,亦即保守力作功等於負的位能變化 :
W
=
−
Δ
U
{\displaystyle W=-\Delta U}
2.非保守力作功時,若有保守力作負功則優先化為位能,剩下的功才化為物體的動能 ,即非保守力作功等於總力學能 (動能+位能)變化 :
W
=
Δ
E
=
Δ
E
k
+
Δ
U
{\displaystyle W=\Delta E=\Delta E_{\rm {k}}+\Delta U}
3.綜合以上兩點,一物體所受的淨力包含了保守力與非保守力,非保守力使總力學能變,而保守力將之部份化為位能,二者相加,即淨力作功等於動能變化 :
W
=
Δ
E
k
{\displaystyle W=\Delta E_{\rm {k}}}
根據這些公式證明功是與作用力相關的能量,所以作功是能被測量的,是一種具有物理單位的能量。
上面所討論的作功、能量原理也適用於非機械能,例如電器和能源等,其原理是相同的。
約束力決定了系統中物件的位移,將其限制在範圍內(以斜面加重力為例,當物體受到無法再伸長的緊繩約束使其不能再下滑,物體就會卡 在斜面上)。它消除了在該方向上所有的位移,即物體平行此力的速度被約束為0,因此約束力不對系統作功 。
例如:用一根繩子系上一個小球作等速率圓周運動,小球會受到來自繩子,方向指向圓心的一個向心力。這個力的方向和球速度的方向垂直,所以這個力不作功(W=0)。又如桌上有一本書,施加外力會使書在桌面上移動。如果再對書施加一個垂直的力(實際上書受到的重力和支持力就屬於這個力),和其欲移動之方向垂直,則此約束力(施加的垂直力)不作功。
磁場中的帶電粒子受到磁力(勞侖茲力)的大小為F = qv×B ,其中q為電荷,v是粒子速度,而B為磁場強度。外積 結果恆垂直於兩原向量,因此F⊥v。而兩垂直向量的內積 恆零,因此磁力作的功W = 0。磁力可改變此粒子運動的方向,但是永遠無法改變運動速率(磁力不作功,動能不變)。帶電粒子在均強磁場中受到與速度方向垂直,固定大小的力,因此粒子會以原來的速率作圓周運動。(質譜儀的原理)
對於一移動的物體而言,作功量/時間可以從距離/時間(即速度
v
{\displaystyle v}
功率 (焦耳/秒、瓦),其值為力的純量積(向量)和作用點上的速度向量。力的純量積和速度被歸類為瞬時功率。
而正如速度可能會隨着時間的推移以獲得更長的距離,同一條路徑上的總功率也同樣是作用點沿着同一條路徑上之瞬時功率的時間積分的總和。
功是指質點受外力作用位移而產生的量,當質點移動時,它沿着曲線
X
{\displaystyle X}
v
{\displaystyle v}
t
{\displaystyle t}
δ
W
{\displaystyle \delta W}
d
t
{\displaystyle \mathrm {d} t}
δ
W
=
F
⋅
d
s
=
F
⋅
v
d
t
{\displaystyle \delta W=\mathbf {F} \cdot \mathrm {d} \mathbf {s} =\mathbf {F} \cdot \mathbf {v} \,\mathrm {d} t}
其中
F
⋅
v
{\displaystyle \mathbf {F} \cdot \mathbf {v} }
d
t
{\displaystyle \mathrm {d} t}
W
=
∫
t
1
t
2
F
⋅
v
d
t
=
∫
t
1
t
2
F
⋅
d
s
d
t
d
t
=
∫
C
F
⋅
d
s
{\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} \,\mathrm {d} t=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot {\frac {\mathrm {d} \mathbf {s} }{\mathrm {d} t}}\,\mathrm {d} t=\int _{C}\mathbf {F} \cdot \mathrm {d} \mathbf {s} }
其中
C
{\displaystyle C}
x
(
t
1
)
{\displaystyle \mathbf {x} (t_{1})}
x
(
t
2
)
{\displaystyle \mathbf {x} (t_{2})}
如果力的方向總是沿着這條線,力的大小為
F
{\displaystyle F}
W
=
∫
C
F
d
s
{\displaystyle W=\int _{C}F\,\mathrm {d} s}
其中
s
{\displaystyle s}
F
{\displaystyle F}
W
=
∫
C
F
d
s
=
F
∫
C
d
s
=
F
s
{\displaystyle W=\int _{C}F\,\mathrm {d} s=F\int _{C}\mathrm {d} s=Fs}
其中
s
{\displaystyle s}
此計算可歸納為恆定力並非沿着線而是沿着質點。在此情況下內積
F
⋅
d
s
=
F
cos
θ
d
s
{\displaystyle \mathbf {F} \cdot \mathrm {d} \mathbf {s} =F\cos \theta \,\mathrm {d} s}
θ
{\displaystyle \theta }
W
=
∫
C
F
⋅
d
s
=
F
s
cos
θ
{\displaystyle W=\int _{C}\mathbf {F} \cdot \mathrm {d} \mathbf {s} =Fs\cos \theta }
一般常見的情況,施加的力和速度向量對物體成
90
∘
{\displaystyle 90^{\circ }}
cos
90
∘
=
0
{\displaystyle \cos 90^{\circ }=0}
此外物體作等速圓周運動受到機械外力作用時,作的功也為0,就像在一理想情況之無摩擦力的離心機中作等速圓周運動一般。
計算功在時間和力作用在一直線路徑上的數值只適用在最簡單的情況下,如上文所述。如果力會變化,或物體沿曲線方向移動,物體可能轉動甚至並非剛性物體,那麼其所作的功只和作用力的角度、路徑有關,並且只有部分的力平行在作用點上形成的速度才作功
(相同方向為正,反方向為負值),此處的力可以被描述為純量或是切線分量的純量。(
F
cos
θ
{\displaystyle F\cos \theta }
θ
{\displaystyle \theta }
至於功最普遍的定義如下:力作功是其沿著作用點上的路徑之切線分量的純量也就是線性積分。
轉矩是從相等但方向相反的力作用於剛性體上兩個不同的點所形成。這些力總和為零,但它會對物體影響形成轉矩Τ ,計算作功形成的轉矩公式為:
δ
W
=
T
⋅
ω
→
δ
t
{\displaystyle \delta W=\mathbf {T} \cdot {\vec {\omega }}\delta t}
T.ω 是作用在時間點δt 上。這些少量的功之和大於剛性體運動軌跡所產生的功。
W
=
∫
t
1
t
2
T
⋅
ω
→
d
t
{\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {T} \cdot {\vec {\omega }}dt}
如果角速度向量保持恆定的方向,那麼可以寫成:
ω
→
=
ϕ
˙
S
{\displaystyle {\vec {\omega }}={\dot {\phi }}\mathbf {S} }
S 。在此情況下,功的轉矩可寫成:
W
=
∫
t
1
t
2
T
⋅
ω
→
d
t
=
∫
t
1
t
2
T
⋅
S
d
ϕ
d
t
d
t
=
∫
C
T
⋅
S
d
ϕ
{\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {T} \cdot {\vec {\omega }}dt=\int _{t_{1}}^{t_{2}}\mathbf {T} \cdot \mathbf {S} {\frac {d\phi }{dt}}dt=\int _{C}\mathbf {T} \cdot \mathbf {S} d\phi }
C 是從φ(t1 ) 到φ(t2 ) 的運動軌跡。此積分取決於φ(t) 的值,因此與路徑相關。如果轉矩T 與角速度向量一致,那麼可寫成:
T
=
τ
S
{\displaystyle \mathbf {T} =\tau \mathbf {S} }
而且若轉矩和角速度是恆定的,那麼功可寫成這個形式:
W
=
∫
t
1
t
2
τ
ϕ
˙
d
t
=
τ
(
ϕ
2
−
ϕ
1
)
{\displaystyle W=\int _{t_{1}}^{t_{2}}\tau {\dot {\phi }}dt=\tau (\phi _{2}-\phi _{1})}
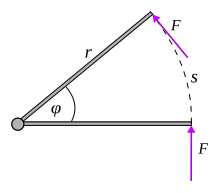
一個大小不變且垂直於槓桿臂的力 此結果可以更簡單的理解,如圖所示。這股力將通過圓弧的距離s=rφ ,所作的功即是:
W
=
F
s
=
F
r
ϕ
{\displaystyle W=Fs=Fr\phi }
τ=Fr ,得:
W
=
F
r
ϕ
=
τ
ϕ
{\displaystyle W=Fr\phi =\tau \phi }
以上,請注意只有轉矩在角速度向量方向的部分才有作功。
力與位移都是向量 。功是力與位移的內積 ,為純量 。
W
=
F
→
⋅
d
→
=
F
d
cos
θ
{\displaystyle W={\vec {F}}\cdot {\vec {d}}=Fd\cos \theta }
其中
θ
{\displaystyle \theta }
夾角 。
為使此式正確,力須為常向量,路徑須為一條直線。
如力隨時間變化或路徑不為直線,上式不再適用,此時需使用曲線積分 。故功的一般公式為:
W
=
∫
C
F
→
⋅
d
x
→
{\displaystyle W=\int _{C}{\vec {F}}\cdot \mathrm {d} {\vec {x}}}
其中
C
{\displaystyle \textstyle _{C}}
F
→
{\displaystyle {\vec {F}}}
x
→
{\displaystyle {\vec {x}}}
表達式
δ
W
=
F
→
⋅
d
s
→
{\displaystyle \delta W={\vec {F}}\cdot \mathrm {d} {\vec {s}}}
非恰當微分 ,
W
C
{\displaystyle \textstyle {W_{C}}}
F
→
⋅
d
x
→
{\displaystyle {\vec {F}}\cdot \mathrm {d} {\vec {x}}}
非零力可以不作功,這一點與衝量 不同。衝量是力對時間的累積。衝量是向量 ,所以圓周運動時雖向心力不作功,但產生了對物體的非零衝量。
力矩 所作功可由下式計算得到:
W
=
τ
θ
{\displaystyle W=\tau \theta \ }
其中
τ
{\displaystyle \tau }
(功)動能定理 (The work–kinetic energy theorem)或稱功能定理(The work–energy theorem)、功能原理(The work–energy principle),意指淨力 作用在物質 上(淨力作功)的功等於物質的動能 變化量。
淨力W 在質點 上所作的功等於其動能的變化量
E
k
{\displaystyle E_{k}}
[ 6]
W
=
Δ
E
k
=
1
2
m
v
2
2
−
1
2
m
v
1
2
{\displaystyle W=\Delta E_{\rm {k}}={\tfrac {1}{2}}mv_{2}^{2}-{\tfrac {1}{2}}mv_{1}^{2}}
v
1
{\displaystyle v_{1}}
v
2
{\displaystyle v_{2}}
速度 和末速度,m則是質量 。
功與能的原理由牛頓第二運動定律 推導,其中包括作用在質點上的淨力和約束反力 對質點造成的位移 量。
對於勻變速直線運動 的情形,推導 如下式。
W
=
F
d
=
m
a
d
=
m
a
(
v
2
2
−
v
1
2
2
a
)
=
m
v
2
2
2
−
m
v
1
2
2
=
Δ
E
k
{\displaystyle W=Fd=mad=ma\left({\frac {v_{2}^{2}-v_{1}^{2}}{2a}}\right)={\frac {mv_{2}^{2}}{2}}-{\frac {mv_{1}^{2}}{2}}=\Delta {E_{k}}}
d
=
v
2
2
−
v
1
2
2
a
{\displaystyle d={\frac {v_{2}^{2}-v_{1}^{2}}{2a}}}
v
2
2
=
v
1
2
+
2
a
d
{\displaystyle v_{2}^{2}=v_{1}^{2}+2ad}
一般情況下的推導則如下式。
W
=
∫
t
1
t
2
F
⋅
v
d
t
=
∫
t
1
t
2
F
v
d
t
=
∫
t
1
t
2
m
a
v
d
t
=
m
∫
t
1
t
2
v
d
v
d
t
d
t
=
m
∫
v
1
v
2
v
d
v
=
1
2
m
(
v
2
2
−
v
1
2
)
{\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} dt=\int _{t_{1}}^{t_{2}}F\,vdt=\int _{t_{1}}^{t_{2}}ma\,vdt=m\int _{t_{1}}^{t_{2}}v\,{dv \over dt}\,dt=m\int _{v_{1}}^{v_{2}}v\,dv={\tfrac {1}{2}}m(v_{2}^{2}-v_{1}^{2})}
^ 1.0 1.1 (日)小幡彩貴,1分鐘懂科學 圖解100個科學基本名詞,海峽書局,2021.09,第15頁
^ NCERT . Physics Book (PDF) . ncert.nic.in. 2020 [24 November 2021] . (原始內容存檔 (PDF) 於2023-10-03). ^ Jammer, Max. Concepts of Force. Dover Publications, Inc. 1957. ISBN 0-486-40689-X ^ Tipler. 1991: 138. ^ 5.0 5.1 Resnick, Robert and Halliday, David. Physics , Section 7-2 (Vol I and II, Combined edition). Wiley International Edition, Library of Congress Catalog Card No. 66-11527. 1966. ^ Hugh D. Young and Roger A. Freedman. University Physics 12th. Addison-Wesley. 2008: 329 . ISBN 978-0-321-50130-1
Serway, Raymond A.; Jewett, John W. Physics for Scientists and Engineers 6th ed. Brooks/Cole. 2004. ISBN 0-534-40842-7 Tipler, Paul. Physics for Scientists and Engineers: Mechanics 3rd ed., extended version. W. H. Freeman. 1991. ISBN 0-87901-432-6
線性(平動)的量
角度(轉動)的量
因次
—
L
L2
因次
—
—
—
T
時間 : t s 位移積分 : A m s T
時間 : t s
—
距離 : d 位矢 : r s x 位移 m 面積 : A m2 —
角度 : θ 角移 : θ rad 立體角 : Ω rad2 , sr
T−1
頻率 : f s−1 Hz 速率 : v 速度 : v m s−1 面積速率 : ν m2 s−1 T−1
頻率 : f s−1 Hz 角速率 : ω 角速度 : ω rad s−1
T−2
加速度 : a m s−2 T−2
角加速度 : α s−2
T−3
加加速度 : j −3 T−3
角加加速度 : ζ s−3
M
質量 : m kg ML2
轉動慣量 : I m2
MT−1
動量 : p 衝量 : J m s−1 , N s 作用量 : 𝒮 actergy : ℵ m2 s−1 , J s ML2 T−1
角動量 : L 角衝量 : ι m2 s−1 作用量 : 𝒮 actergy : ℵ m2 s−1 , J s
MT−2
力 : F 重量 : F g kg m s−2 , N 能量 : E 功 : W kg m2 s−2 , J ML2 T−2
力矩 : τ moment M kg m2 s−2 , N m 能量 : E 功 : W kg m2 s−2 , J
MT−3
加力 : Y kg m s−3 , N s−1 功率 : P kg m2 s−3 , W ML2 T−3
rotatum P kg m2 s−3 , N m s−1 功率 : P kg m2 s−3 , W